Se denomina geometría no euclidiana o no euclídea, a cualquier forma de geometría cuyos postulados y propiedades difieren en algún punto de los establecidos por Euclides en su tratado Elementos. No existe un sólo tipo de geometría no euclídea, sino muchos, aunque si se restringe la discusión a espacios homogéneos, en los que la curvatura del espacio la misma en cada punto, en los que los puntos del espacio son indistinguibles pueden distinguirse tres tipos de geometrías:
- La geometría euclideana satisface los cinco postulados de Euclides y tiene curvatura cero.
- La geometría hiperbólica satisface sólo los cuatro primeros postulados de Euclides y tiene curvatura negativa.
- La geometría elíptica satisface sólo los cuatro primeros postulados de Euclides y tiene curvatura positiva.
Todos estos son casos particulares de geometrías riemannianas, en los que la curvatura es constante, si se admite la posibilidad de que la curvatura intrínseca de la geometría varíe de un punto a otro se tiene un caso de geometría riemanniana general, como sucede en la teoría de la relatividad general donde la gravedad causa una curvatura no homogénea en el espacio tiempo, siendo mayor la curvatura cerca de las concentraciones de masa, lo cual es percibido como un campo gravitatoria atractivo.
Contenido[ocultar] |
[editar]Historia
El primer ejemplo de geometría no euclidiana fue la hiperbólica, teorizada inicialmente por Immanuel Kant[cita requerida], formalizada posterior e independientemente por varios autores a principios del siglo XIX tales como Carl Friedrich Gauss, Nikolái Lobachevski, János Bolyai y Ferdinand Schweickard.
Los desarrollos de geometrías no euclídeas se gestaron en sus comienzos con el objetivo de construir modelos explícitos en los que no se cumpliera el quinto postulado de Euclides.
La geometría Euclideana había sido desarrollada por los griegos y expuesta por Euclides en la obra Los elementos. En su primera obra publicada, "Pensamientos sobre la verdadera estimación de las fuerzas vivas" (Gedanken von der wahren Schätzung der lebendigen Kräfte und Beurteilung der Beweise derer sich Herr von Leibniz und anderer Mechaniker in dieserStreitsache bedient haben) (1746), Immanuel Kant considera espacios de más de tres dimensiones y afirma:
Una ciencia de todas estas posibles clases de espacio sería sin duda la empresa más elevada que un entendimiento finito podría acometer en el campo de la Geometría... Si es posible que existan extensiones con otras dimensiones, también es muy probable que Dios las haya traído a la existencia, porque sus obras tienen toda la magnitud y variedad de que son capaces.
Esas posibles geometrías que Kant entrevé son las que hoy se llaman geometrías euclidianas de dimensión mayor que 3.
Por otra parte, ya desde la antigüedad se consideró que el quinto postulado del libro de Euclides no era tan evidente como los otros cuatro pues, al afirmar que ciertas rectas no se cortarán al prolongarlas indefinidamente, habla de una construcción mental un tanto abstracta. Por eso durante muchos siglos se intentó sin éxito demostrarlo a partir de los otros cuatro. A principios del siglo XIX, se intentó demostrarlo por reducción al absurdo, suponiendo que es falso y tratando de obtener una contradicción. Sin embargo, lejos de llegar a un absurdo se encontró que existían geometrías coherentes diferentes de la euclídea. Se había descubierto así la primera geometría no euclídea (en concreto el primer ejemplo que se logró era una geometría llamada hiperbólica).
[editar]Geometrías de curvatura constante
[editar]Geometría hiperbólica
A principios del siglo XIX, y de modo independiente, Gauss (1777-1855), Lobachevsky (1792-1856), János Bolyai y Ferdinand Schweickard lograron construir la geometría hiperbólica, a partir del intento de negar el quinto postulado de Euclides y tratar de obtener una contradicción. En lugar de obtener una contradicción lo que obtuvieron fue una curiosa geometría en la que los tres ángulos de un triángulo sumaban menos de 180º sexagesimales (en la geometría euclídea los ángulos de cualquier triángulo suman siempre exactamente 180º).
La naturalidad de esta geometría quedó confirmada a finales del siglo, cuando Beltrami demostró que la geometría hiperbólica coincide con la geometría intrínseca de cierta superficie y Klein dio la interpretación proyectiva de la geometría hiperbólica. Ambos resultados prueban que es tan consistente como la Geometría euclídea (es decir, si la geometría hiperbólica lleva a alguna contradicción, entonces la geometría euclídea también).
Algunos afirman que Gauss fue el primero en considerar la posibilidad de que la geometría del Universo no fuera la euclídea. Sabiendo que en la geometría hiperbólica la suma de los ángulos de cualquier triángulo es menor que dos rectos, se dice que subió a la cima de tres montañas con un teodolito, aunque la precisión de sus instrumentos no fue suficiente para decidir la cuestión con tal experimento. Sin embargo, otros afirman que cuando escribió que trataba de corregir los efectos de posibles curvaturas se refería a corregir el efecto de la curvatura terrestre en los estudios cartográficos que estaba realizando.
[editar]Geometría elíptica
La geometría elíptica es el segundo tipo de geometría no-euclídea homogénea, es decir, donde cualquier punto resulta del espacio resulta indistinguible de cualquier otro. Una variedad de Riemann de curvatura positiva constante es un ejemplo de geometría elíptica. Un modelo clásico de geometría elíptica n-dimensional es la n-esfera.
En la geometria elíptica las líneas geodésicas tienen un papel similar a las líneas rectas de la geometría euclídea, con algunas importanes diferencias. Si bien la mínima distancia posible entre dos puntos viene dada por una línea geodésica, que además son líneas de curvatura mínima, el quinto postulado de Euclídes no es válido para la geometría elíptica, ya que dada una "recta" de esta geometría (es decir, una línea geodésica) y un punto no contenido en la misma no se puede trazar ninguna geodésica que no corte a la primera.
[editar]Geometría euclídea
La geometría euclídea es claramente un caso límite intermedio entre la geometría elíptica y la geometría hiperbólica. De hecho la geometría euclídea es una geometría de curvatura nula. Puede demostrarse que cualquier espacio geométrico o variedad de Riemann cuya curvatura es nula es localmente isométrico al espacio euclídeo y por tanto es un espacio euclídeo o idéntico a una porción del mismo.
[editar]Aspectos matemáticos
Los espacios de curvatura constante el tensor de curvatura de Riemann viene dado en componentes por la siguiente expresión:
donde  es el tensor métrico expresado en coordenadas curvilíneas cualesquiera. En tensor de Ricci
es el tensor métrico expresado en coordenadas curvilíneas cualesquiera. En tensor de Ricci 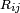 y la curvatura escalar
y la curvatura escalar  son proporcionales respectivamente al tensor métrico y a la curvatura:
son proporcionales respectivamente al tensor métrico y a la curvatura:
 es el tensor métrico expresado en coordenadas curvilíneas cualesquiera. En tensor de Ricci
es el tensor métrico expresado en coordenadas curvilíneas cualesquiera. En tensor de Ricci 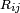 y la curvatura escalar
y la curvatura escalar  son proporcionales respectivamente al tensor métrico y a la curvatura:
son proporcionales respectivamente al tensor métrico y a la curvatura:y donde  es la dimensión del espacio.
es la dimensión del espacio.
 es la dimensión del espacio.
es la dimensión del espacio.Otro aspecto interesante es que tanto en la geometría hiperbólica, como en la geometría elíptica homogéneas el grupo de isometría del espacio completo es un grupo de Lie de dimensión 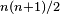 , que coincide con la dimensión del grupo de isometría de un espacio Euclideo de dimensión n (aunque los tres grupos son diferentes).
, que coincide con la dimensión del grupo de isometría de un espacio Euclideo de dimensión n (aunque los tres grupos son diferentes).
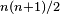 , que coincide con la dimensión del grupo de isometría de un espacio Euclideo de dimensión n (aunque los tres grupos son diferentes).
, que coincide con la dimensión del grupo de isometría de un espacio Euclideo de dimensión n (aunque los tres grupos son diferentes).[editar]Geometrías de curvatura no constante
[editar]Geometría riemanniana general
A propuesta de Gauss, la disertación de Riemann versó sobre la hipótesis de la Geometría. En su tesis, Riemann considera las posibles geometrías que infinitesimalmente (i.e. en regiones muy pequeñas) sean euclídeas, cuyo estudio se conoce hoy en día como geometrías riemannianas. Estas geometrías resultan en general no-homogéneas: algunas de las propiedades del espacio pueden diferir de un punto a otro, en particular el valor de la curvatura.
Para el estudio de estas geometrías Riemann introdujo el formalismo del tensor de curvatura y demostró que la geometría euclídea, la geometría hiperbólica y la geometría elíptica son casos particulares de geometrías riemanninanas, caracterizadas por valores constantes del tensor de curvatura. En una geometría riemanninana general, el tensor de curvatura tendrá valores variables a lo largo de diferentes puntos de dicha geometría.
Eso hace que la geometría no sea homogénea, y permite distinguir unos puntos de otros. Esto es relevante en la teoría de la relatividad general, ya que en principio es posible hacer experimentos de medición de distancias y ángulos que permitan distinguir unos puntos del espacio de otros, tal como especifican numerosos experimentos mentales imaginados por Einstein y otros en los que un experimentador encerrado en una caja puede realizar experimentos para decidir la naturaleza del espacio-tiempo que le rodea.
Finalmente un aspecto interesante de la goemetría riemanniana es que si la curvatura no es constante entonces el grupo de isometría del espacio tiene dimensión estrictamente menor que 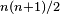 siendo
siendo  la dimensión del espacio. En concreto según la relatividad especial un espacio-tiempo con una distribución muy irregular de la materia podría tener un grupo de isometría trivial de dimensión 0.
la dimensión del espacio. En concreto según la relatividad especial un espacio-tiempo con una distribución muy irregular de la materia podría tener un grupo de isometría trivial de dimensión 0.
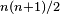 siendo
siendo  la dimensión del espacio. En concreto según la relatividad especial un espacio-tiempo con una distribución muy irregular de la materia podría tener un grupo de isometría trivial de dimensión 0.
la dimensión del espacio. En concreto según la relatividad especial un espacio-tiempo con una distribución muy irregular de la materia podría tener un grupo de isometría trivial de dimensión 0.[editar]Geometría del espacio-tiempo y teoría de la relatividad
Basándose en la ideas y resultados de Riemann, hacia 1920 Einstein aborda en su Teoría de la Relatividad general la cuestión de la estructura geométrica del Universo. En ella muestra cómo la geometría del espacio-tiempo tiene curvatura, que es precisamente lo que se observa como campo gravitatorio, y cómo, bajo la acción de la gravedad, los cuerpos siguen las líneas más rectas posibles dentro de dicha geometría, líneas que se denominan geodésicas.
Además, la Ecuación de Einstein afirma que para cada observador, la curvatura media del espacio coincide, salvo un factor constante, con la densidad observada, dando cumplimiento así a la fantástica visión de Gauss: la geometría desentrañada por los griegos es la estructura infinitesimal del espacio; al generalizar dicha estructura geométrica, tiene curvatura.
Los tres tipos de geometrías homogéneas posibles, además de la geometría euclidea de curvatura nula, existen la geometría elíptica de curvatura positiva, y lageometría hiperbólica de curvatura negativa. Si se consideran geometrías no-euclídeas homogéneas entonces existe una infinidad de posibles geometrías, descritas por las variedades riemannianas generales.




No hay comentarios:
Publicar un comentario