Teoría de Grupos


En álgebra abstracta, la teoría de grupos estudia las estructuras algebraicas conocidas como grupos. Sus objetivos son, entre otros, la clasificación de los grupos, sus propiedades y sus aplicaciones tanto dentro como fuera de las matemáticas.
Los grupos sirven como pilar a otras estructuras algebraicas más elaboradas como los anillos, los cuerpos o los espacios vectoriales. La teoría de grupos tiene muchas aplicaciones en el campo de la física y la química, y es potencialmente aplicable en situaciones caracterizadas por la simetría.
El orden de un grupo es su cardinalidad; en base a él, los grupos pueden clasificarse en grupos de orden finito de orden infinito. La clasificación de los grupos simples de orden finito es uno de los mayores logros matemáticos del siglo XX.

Contenido

 [ocultar]

[editar]
Historia

Las raíces históricas de la teoría de grupos son la teoría de las ecuaciones algebraicas, la teoría de números y la geometría. Euler, Gauss, Lagrange, Abel y Galois fueron los investigadores iniciadores de ésta ciencia. Galois es reconocido como el primer matemático que relacionó ésta teoría con la teoría de cuerpos resultando en la teoría de Galois. Otros importantes matemáticos en este campo incluyen a Cayley, Emil Artin, Emmy Noether, Sylow entre muchos otros. Fue Walter von Dick quién en 1882, dio la moderna definición de grupo.

[editar]
Definiciones

[editar]
Grupos

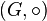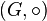Un grupo (G, \circ) es un conjunto G en el que se ha definido una ley de composición interna \circ que satisface los siguientes axiomas:
  1. Asociatividad: a \circ (b \circ c)=(a \circ b) \circ c, \forall a,b,c \in G
  2. Elemento neutro: \exists e \in G : e \circ a=a \circ e=a
  3. Elemento simétrico: \forall a \in G\quad \exists a^{-1} \in G : a\circ a^{-1}=a^{-1} \circ a=e
Por lo tanto, un grupo está formado por un conjunto de objetos abstractos o símbolos, y por una ley de composición interna que los relaciona. Dicha ley de composición interna indica cómo deben ser manipulados los objetos del grupo.
Se dice que un grupo es abeliano o conmutativo cuando verifica además la propiedad conmutativa:
a \circ b = b \circ a \quad \forall a \in G

[editar]
Notación

Se habla de notación aditiva cuando se representa la ley de composición interna como "a + b", y el elemento neutro como " 0 ". Por otro lado, la notación multiplicativa es aquella en la que la ley de composición interna se representa como "a \cdot b", o "ab", y el elemento neutro como " 1 ".

[editar]
Ejemplos

  • (\mathbb{Z},+), el conjunto de números enteros con la suma usual, es un grupo abeliano; donde el elemento neutro es el 0, y el simétrico de x, es -x.
  • (\mathbb{R},+), el conjunto de los números reales con la suma usual, es un grupo abeliano; donde el elemento neutro es el 0, y el simétrico de x, es -x.
  • (\mathbb{R}\setminus\{0\},\cdot), el conjunto de los números reales (excluyendo al 0) con la multiplicación, es un grupo abeliano; donde el elemento neutro es el 1, y el simétrico de x es 1/x. Notar que al no tener el cero elemento simétrico multiplicativo, se lo debe excluir.
  • El conjunto de todas las biyecciones de un conjunto X - simbolizado por S(X) - junto con la composición de funciones, es un grupo no abeliano (si la cardinalidad de X es mayor que dos) y se llama grupo simétrico de X.
  • El conjunto de matrices rectangulares de dimensiones n\times m con la suma, es un grupo abeliano.
  • El conjunto de matrices cuadradas con determinante diferente de cero con la multiplicación (Grupo general lineal), no es abeliano.
  • Las clases de homotopía de trayectorias continuas S^1\to X en un espacio topológico X forman un grupo no necesariamente abeliano. Ésta construcción es el grupo fundamental de X.
    • El grupo fundamental de un círculo (circle, cercle, Kreis) es el grupo cíclico infinito; \mathbb{Z}.
    • El de la esfera S2 es trivial = 0.
    • De un toro es \mathbb{Z}\oplus \mathbb{Z}
    • De un toro sin un disco es el grupo libre de orden dos, F2. De un toro sin dos discos disjuntos; F3.
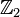
    • Del plano proyectivo es \mathbb{Z}_2
    • El de la botella de Klein tiene la presentación; \langle a,b: aba=b\rangle y que corresponde al producto semidirecto de \mathbb{Z} con \mathbb{Z}.

[editar]
Operaciones

Entre dos grupos G, H puede haber morfismos, i.e. funciones que son compatibles con las operaciones en cada uno de ellos. Si \phi\colon G\to H es un homomorfismo entonces obedece
\phi(ab)=\phi(a)\phi(b)\,
donde hemos hecho la convención de escribir ab para indicar la operación de a con b en G, y φ(a)φ(b) la operación de φ(a) con φ(b) en H.
El conjunto φS es un subgrupo en H cuando S es un subgrupo en G.
Si transformamos un conmutador: aba − 1b − 1 se obtiene: φ(aba − 1b − 1) = φ(a)φ(b)(φ(a)) − 1(φ(b)) − 1.

[editar]
Categoría de grupos

Desde el punto de vista de la teoría de categorías, la teoría de grupos podría catalogarse como una categoría llamada categoría de grupos, debido a que en ella se estudia a los grupos y sus morfismos. La categoría de grupos es muy grande, pero puede armarse una relación de equivalencia en esta categoría para que se factorice: la relación entre grupos de serisomorfos reduce cuestiones estructurales de la categoría de grupos a la categoría de grupos-módulo-los-isomorfos. En esta reducción la operación de unión disjunta la convierte en unacategoría monoidal.

[editar]
Teoría geométrica de los grupos

Los más actuales temas de investigación en la teoría de grupos tienen que ver con las modernas técnicas de la topología. Una manera estándar de construir nuevos grupos a partir de los conocidos son los
  • productos libres,
  • productos libres amalgamados y las
  • HNN-extensiones.
La gran variedad de técnicas topológicas pueden ser aplicadas desde que se sabe que es posible construir siempre un espacio topológico (de hecho un CW-complejo dos-dimensional) de tal manera que el grupo fundamental de este espacio es el grupo dado.


No hay comentarios:

Publicar un comentario

Suscribirse a: Enviar comentarios (Atom)