En análisis matemático, el teorema de la función implícita establece condiciones bajo las cuales una ecuación de varias variables permite definir a una de ellas como función de las demás.
Una función y(x) está dada de forma implícita cuando está definida de la forma F (x, y) = 0 en lugar de la habitual. Dada la ecuación F(x,y)=0(lo que se conoce como función implícita), bajo ciertas exigencias sobre la derivada de F podríamos, al menos localmente, despejar y=f(x). Por ejemplo, puede probarse que la siguiente ecuación define una función implícita en cierta región de  entre las variables x e y:
entre las variables x e y:
 entre las variables x e y:
entre las variables x e y:Contenido[ocultar] |
[editar]Enunciado General
Antes de enunciar el teorema, considere la función f(x,y) = 0 que definiremos:
La función admite como preimagenes todos los vectores (x,y) que resuelven la ecuación  . Por esto, no es posible despejar globalmente una variable en términos de la otra y por lo mismo no es posible determinar cómo cambia una variable en función de la otra, al menos no globalmente pero si en una vecindad de (x0,y0).
. Por esto, no es posible despejar globalmente una variable en términos de la otra y por lo mismo no es posible determinar cómo cambia una variable en función de la otra, al menos no globalmente pero si en una vecindad de (x0,y0).
 . Por esto, no es posible despejar globalmente una variable en términos de la otra y por lo mismo no es posible determinar cómo cambia una variable en función de la otra, al menos no globalmente pero si en una vecindad de (x0,y0).
. Por esto, no es posible despejar globalmente una variable en términos de la otra y por lo mismo no es posible determinar cómo cambia una variable en función de la otra, al menos no globalmente pero si en una vecindad de (x0,y0).El enunciado general es como sigue:
Teorema (de la Función Implícita): Sean  una función continua y diferenciable y
una función continua y diferenciable y  cualquier vector tal que f(a,b) = 0 . Considere
cualquier vector tal que f(a,b) = 0 . Considere  y defina la matriz jacobiana DF(a,b) = [Dxf(a,b),Dyf(a,b)] y sobre esta considere que la submatriz que define [Dyf(a,b)] es invertible. Entonces existen los abiertos
y defina la matriz jacobiana DF(a,b) = [Dxf(a,b),Dyf(a,b)] y sobre esta considere que la submatriz que define [Dyf(a,b)] es invertible. Entonces existen los abiertos  y
y  con
con  y
y  tales que para cada
tales que para cada 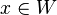 existe un único y tal que
existe un único y tal que  y f(x,y) = 0 lo que define una función
y f(x,y) = 0 lo que define una función 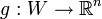 que es continua y diferenciable y que además satisface
que es continua y diferenciable y que además satisface
 una función continua y diferenciable y
una función continua y diferenciable y  cualquier vector tal que f(a,b) = 0 . Considere
cualquier vector tal que f(a,b) = 0 . Considere  y defina la matriz jacobiana DF(a,b) = [Dxf(a,b),Dyf(a,b)] y sobre esta considere que la submatriz que define [Dyf(a,b)] es invertible. Entonces existen los abiertos
y defina la matriz jacobiana DF(a,b) = [Dxf(a,b),Dyf(a,b)] y sobre esta considere que la submatriz que define [Dyf(a,b)] es invertible. Entonces existen los abiertos  y
y  con
con  y
y  tales que para cada
tales que para cada 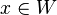 existe un único y tal que
existe un único y tal que  y f(x,y) = 0 lo que define una función
y f(x,y) = 0 lo que define una función 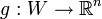 que es continua y diferenciable y que además satisface
que es continua y diferenciable y que además satisfaceademás
donde g(a) = b.
La demostración del teorema se puede encontrar en diversos libros de cálculo, en particular el final del artículo se presenta un enlace a una demostración con detalles. Las versiones del teorema en dos dimensiones resultan útiles para fijar ideas antes de extenderse al caso de "n" dimensiones.
[editar]Diferenciación de Funciones dadas de forma implícita
Para poder derivar una función implícita se usa la Regla de la cadena, en el caso de la variable independiente no hay problema ya que se deriva directamente, para la variable dependiente se considera como una función que a su vez está en función de la variable independiente:
Dada una función  , implícita, si queremos calcular la derivada de y respecto de x:
, implícita, si queremos calcular la derivada de y respecto de x:  .
.
 , implícita, si queremos calcular la derivada de y respecto de x:
, implícita, si queremos calcular la derivada de y respecto de x:  .
.Si consideramos 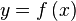 es una función en términos de la variable independiente x y
es una función en términos de la variable independiente x y  es una función en términos de la variable dependiente y, dado que
es una función en términos de la variable dependiente y, dado que 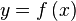 , entonces para obtener la derivada:
, entonces para obtener la derivada:
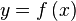 es una función en términos de la variable independiente x y
es una función en términos de la variable independiente x y  es una función en términos de la variable dependiente y, dado que
es una función en términos de la variable dependiente y, dado que 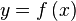 , entonces para obtener la derivada:
, entonces para obtener la derivada:[editar]Ejemplo
Obtener la derivada de:
El término 6x2y Se puede considerar que son dos funciones, 6x2 y y por lo que se derivara como un producto:
El término 5y3 se deriva como:
El término 3x2 se deriva de forma normal como:
El valor constante 12, que no depende ni de x ni de y, tiene por derivada 0, como corresponde a un valor constante.
Para el término x2y2 se puede considerar como un producto y se deriva como:
Al unir todos los términos se obtiene:
Ordenando
Factorizando respecto a ( 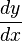 ) los valores son:
) los valores son:
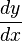 ) los valores son:
) los valores son:Finalmente despejando 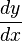 se obtiene la derivada de la función implícita:
se obtiene la derivada de la función implícita:
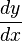 se obtiene la derivada de la función implícita:
se obtiene la derivada de la función implícita:





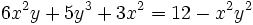
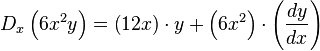




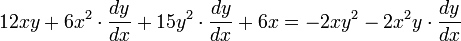
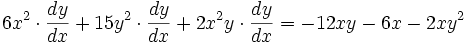

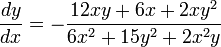



No hay comentarios:
Publicar un comentario