Se denomina sección cónica (o simplemente cónica) a la intersección de un cono circular recto de dos hojas con un plano que no pasa por su vértice. Se clasifican en tres tipos: elipse, parábola e hipérbola.
Contenido[ocultar] |
[editar]Etimología
La primera definición conocida de sección cónica surge en la Antigua Grecia, cerca del año 350 (Menæchmus) donde las definieron como secciones «de un cono circular recto».1 Los nombres de hipérbola, parábola y elipse se deben a Apolonio de Perge. Actualmente, las secciones cónicas pueden definirse de varias maneras; estas definiciones provienen de las diversas ramas de la matemática (como la geometría analítica), la (geometría proyectiva), etc.)
[editar]Tipos
En función de la relación existente entre el ángulo de conicidad (α) y la inclinación del plano respecto del eje del cono (β), pueden obtenerse diferentes secciones cónicas, a saber:
- β < α : Hipérbola (azul)
- β = α : Parábola (verde)
- β > α : Elipse (amarillo)
- β = 90º: Circunferencia (un caso particular de elipse) (rojo)
Si el plano pasa por el vértice del cono, se puede comprobar que:
- Cuando β > α la intersección es un único punto (el vértice).
- Cuando β = α la intersección es una recta generatriz del cono (el plano será tangente al cono).
- Cuando β < α la intersección vendrá dada por dos rectas que se cortan en el vértice.
- cuando β = 90 El ángulo formado por las rectas irá aumentando a medida β disminuye, hasta alcanzar el máximo (α) cuando el plano contenga al eje del cono (β = 0).
[editar]Expresión algebraica
En coordenadas cartesianas, las cónicas se expresan en forma algebraica mediante ecuaciones cuadráticas de dos variables (x,y) de la forma:
en la que, en función de los valores de los parámetros, se tendrá:
- h² > ab: hipérbola.
- h² = ab: parábola.
- h² < ab: elipse.
- a = b y h = 0: circunferencia .
[editar]Características
La elipse es el lugar geométrico de los puntos del plano tales que la suma de las distancias a dos puntos fijos llamados focos es constante.
Además de los focos F y F´, en una elipse destacan los siguientes elementos:
- Centro, O
- Eje mayor, AA´
- Eje menor, BB´
- Distancia focal, OF
La elipse tiene la siguiente expresión algebraica: 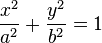
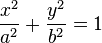
La hipérbola es el lugar geométrico de los puntos del plano cuya diferencia de distancias a dos puntos fijos, llamados focos, es constante y menor que la distancia entre los focos.
Tiene dos asíntotas (rectas cuyas distancias a la curva tienden a cero cuando la curva se aleja hacia el infinito). Las hipérbolas cuyas asíntotas son perpendiculares se llaman hipérbolas equiláteras.
Además de los focos y de las asíntotas, en la hipérbola destacan los siguientes elementos:
- Centro, O
- Vértices, A y A
- Distancia entre los vértices
- Distancia entre los focos
La ecuación de una hipérbola con centro (0, 0), es: 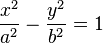
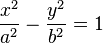
La parábola es el lugar geométrico de los puntos del plano que equidistan de un punto fijo llamado foco, y de una recta llamada directriz.
Además del foco, F, y de la directriz, d, en una parábola destacan los siguientes elementos:
- Eje, e
- Vértice, V
- Distancia de F a d, p.
Una parábola, cuyo vértice está en el origen y su eje coincide con el de ordenadas, tiene la siguiente ecuación: 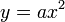
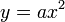
[editar]Aplicaciones
Las curvas cónicas son importantes en astronomía: dos cuerpos masivos que interactúan según la ley de gravitación universal, sus trayectorias describen secciones cónicas si su centro de masa se considera en reposo. Si están relativamente próximas describirán elipses, si se alejan demasiado describirán hipérbolas o parábolas.
También son importantes en aerodinámica y en su aplicación industrial, ya que permiten ser repetidas por medios mecánicos con gran exactitud, logrando superficies, formas y curvas perfectas.


No hay comentarios:
Publicar un comentario