Una deducción o demostración matemática es una sucesión coherente de pasos que, tomando como verdadero un conjunto de premisas llamado hipótesis, permite asegurar la veracidad de una tesis. Estos pasos deben estar fundamentados en la aplicación de reglas de deducción (fundadas ya sea en axiomas o en teoremas anteriormente demostrados o en reglas básicas de deducción del sistema en cuestión). El hecho de no conocer ninguna demostración de un teorema no implica su no veracidad; sólo la demostración de la negación de este resultado implica que es falso.
Aunque en general no existe un procedimiento único de demostración de teoremas, sí existen diferentes tipos de demostraciones que son utilizados comúnmente en matemáticas:
- Demostración por contraposición(formalizado y utilizado, en los silogismos, por Aristóteles)
- Demostración por reducción al absurdo(formalizado y utilizado por Aristóteles), y como caso particular, descenso infinito
- Inducción matemática
Por otra parte, a pesar del alto grado de intervención humana necesario para hacer una demostración, también existen técnicas computacionales que permiten hacer demostraciones automáticas, notablemente en el campo de la geometría euclidiana.
Contenido[ocultar] |
[editar]Ejemplo de una demostración por contradicción
Llamada también demostración al absurdo
Demostración de la afirmación 

Antes de demostrar esto debemos tener claro que existen ciertos axiomas que nos permitirán, en este caso, demostrar nuestra afirmación. Dado que nos basaremos en axiomas, tenemos que nuestra demostración (siendo cada paso lógico correcto) es verdadera.
- Usaremos los siguientes Axiomas de los Números Reales:
- 1.

- 2. Si
 y
y  , con a,b,c reales. Entonces
, con a,b,c reales. Entonces
Asumidos ciertos estos axiomas podemos comenzar con nuestra demostración.
Supongamos que  como:
como:
 como:
como: , aplicando el axioma 2 al multiplicar por 1 (que es menor que cero), tenemos que
, aplicando el axioma 2 al multiplicar por 1 (que es menor que cero), tenemos que , lo cual es una contradicción.
, lo cual es una contradicción.
Como nuestra hipótesis era que  , y ésta es falsa, lo único que ahora podemos decir es que
, y ésta es falsa, lo único que ahora podemos decir es que  . Pero el axioma 1 dice que
. Pero el axioma 1 dice que 
 , y ésta es falsa, lo único que ahora podemos decir es que
, y ésta es falsa, lo único que ahora podemos decir es que  . Pero el axioma 1 dice que
. Pero el axioma 1 dice que 
Luego
- Razonamiento
Es claro que lo que debemos tener es una contradicción. Para ello, primero debemos plantear una hipótesis, y comprobar si es cierta o no. De no serla nos conducirá a una contradicción. Debe tenerse claro que nuestra hipótesis comienza cuando decimos que 1 es menor que cero y no en los axiomas mencionados anteriormente (porque éstos están ya demostrados o bien, asumidos ciertos y no requieren, por lo tanto, mayor análisis). Como sabemos que la afirmación "'1 es menor que cero" es falsa, debiéramos llegar a una contradicción. Pero no basta sólo con saberlo, ya que debe ser demostrado.
Nuestra hipótesis fue que uno era menor que cero y, luego de ciertos pasos lógicos correctos usando los axiomas, concluimos que uno era mayor que cero, lo cual claramente no puede ser cierto, ya que por la ley de tricotomía, dos números reales deben cumplir una y sólo una de las siguientes relaciones
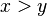 ;
;  o bien
o bien  ,
,
pero nunca dos ni tres juntas. Luego, como nuestra hipótesis nos conduce a una contradicción, es falsa, y debemos considerar todas las posibilidades, menos esa. Esto es: como unono es menor que cero, debe, necesariamente, ser mayor o igual que éste (cero). Pero el axioma primero dice que uno es distinto de cero, por lo que sólo queda la opción de que 1 sea mayor que cero
- Razonamiento incorrecto
Un error común entre quienes comienzan el estudio de estas materias, es el de pensar que han llegado a una contradicción sin haberlo hecho. Por ejemplo: Suponen que:
 , Luego sumando (-1) a ambos lados
, Luego sumando (-1) a ambos lados lo cual es una contradicción ya que
lo cual es una contradicción ya que  .
.
Este razonamiento tiene un error, ya que no llegamos a una contradicción. Nuestra hipótesis era que 1 era menor que cero y por lo tanto, con los procedimientos realizados 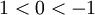 , que es verdadero. En esta caso la afirmación
, que es verdadero. En esta caso la afirmación  es falsa.
es falsa.
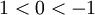 , que es verdadero. En esta caso la afirmación
, que es verdadero. En esta caso la afirmación  es falsa.
es falsa.Nótese que para llegar a una contradicción debemos tener lo siguiente:
- Una afirmación P (en nuestra hipótesis) que diga que ésta es cierta.
- Una conlcusión que diga que P es falsa.
Claramente ninguna afirmación puede cumplir con esto. En lógica esto la afirmación sería:
P es cierta y ~P es cierta, que se lee "P es cierta y no P es cierta".
[editar]Ejemplo de una demostración por inducción
Demostrar que

Demostración
- Debemos comprobar si la afirmación es cierta para
 , ya que la sumatoria parte desde
, ya que la sumatoria parte desde 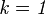 .
.
Sea  , entonces
, entonces
 , entonces
, entonces .
.y la afirmación es cierta para  .
.
 .
.- Supongamos ahora, que la afirmación es cierta para un
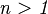 fijo, y veamos que sucede para
fijo, y veamos que sucede para 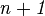 .
.
Por propiedad de las sumatorias tenemos que

como la afirmación es cierta para 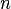 , tenemos que
, tenemos que
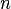 , tenemos que
, tenemos que
ordenando



como 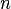 es distinto de
es distinto de 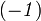 , pordemos simplificar y
, pordemos simplificar y
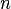 es distinto de
es distinto de 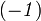 , pordemos simplificar y
, pordemos simplificar y
que es lo que queríamos demostrar.
Así, la afirmación también es verdadera para 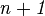 .
.
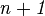 .
.Luego, la afirmación es cierta para todo  .
.
 .
.- Razonamiento
El principio de Inducción dice que dada una afirmación 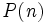 , ésta sera cierta sólo si se cumple que
, ésta sera cierta sólo si se cumple que
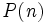 , ésta sera cierta sólo si se cumple que
, ésta sera cierta sólo si se cumple que es cierta
es cierta- Si
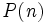 es cierta, entonces
es cierta, entonces  también lo es.
también lo es.
Entonces, como nuestro 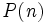 es lo que queremos demostrar, debemos ver si es cierta para su primer término. En este caso para
es lo que queremos demostrar, debemos ver si es cierta para su primer término. En este caso para  .
.
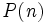 es lo que queremos demostrar, debemos ver si es cierta para su primer término. En este caso para
es lo que queremos demostrar, debemos ver si es cierta para su primer término. En este caso para  .
.Nótese que no necesariamente nos debe quedar 1 en la sumatoria. Lo que nos indica el  es que debemos ver si es cierta para el primer término. Como la afirmación se cumplía para
es que debemos ver si es cierta para el primer término. Como la afirmación se cumplía para  , el paso siguiente era ver si, asumida cierta para
, el paso siguiente era ver si, asumida cierta para 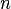 , se cumplía para
, se cumplía para 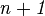 . Así entonces, usamos lo que queremos ver si es cierto en el único miembro de la izquierda de nuestra ecuación. Luego aplicando propiedades de la sumatoria, podemos descomponer la sumatoria en partes y dejar lo que sabemos que es cierto, separado de lo que se puede aplicar por definición. Sabemos que es cierto para
. Así entonces, usamos lo que queremos ver si es cierto en el único miembro de la izquierda de nuestra ecuación. Luego aplicando propiedades de la sumatoria, podemos descomponer la sumatoria en partes y dejar lo que sabemos que es cierto, separado de lo que se puede aplicar por definición. Sabemos que es cierto para 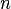 , por lo tanto el primer miembro del lado derecho lo podemos sustituir, mientras que al segundo miembro sólo aplicamos la definición de sumatoria.
, por lo tanto el primer miembro del lado derecho lo podemos sustituir, mientras que al segundo miembro sólo aplicamos la definición de sumatoria.
 es que debemos ver si es cierta para el primer término. Como la afirmación se cumplía para
es que debemos ver si es cierta para el primer término. Como la afirmación se cumplía para  , el paso siguiente era ver si, asumida cierta para
, el paso siguiente era ver si, asumida cierta para 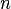 , se cumplía para
, se cumplía para 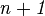 . Así entonces, usamos lo que queremos ver si es cierto en el único miembro de la izquierda de nuestra ecuación. Luego aplicando propiedades de la sumatoria, podemos descomponer la sumatoria en partes y dejar lo que sabemos que es cierto, separado de lo que se puede aplicar por definición. Sabemos que es cierto para
. Así entonces, usamos lo que queremos ver si es cierto en el único miembro de la izquierda de nuestra ecuación. Luego aplicando propiedades de la sumatoria, podemos descomponer la sumatoria en partes y dejar lo que sabemos que es cierto, separado de lo que se puede aplicar por definición. Sabemos que es cierto para 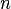 , por lo tanto el primer miembro del lado derecho lo podemos sustituir, mientras que al segundo miembro sólo aplicamos la definición de sumatoria.
, por lo tanto el primer miembro del lado derecho lo podemos sustituir, mientras que al segundo miembro sólo aplicamos la definición de sumatoria.Luego, sumando las fracciones y agrupando, concluímos que el primer miembro del lado izquierdo de nuestra ecuación, se puede expresar como lo que queremos demostrar. Por lo tanto, concluímos que la afirmación es cierta para 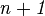 .
.
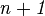 .
.[editar]Definición formal
En lógica matemática y en lógica proposicional, una demostración es una secuencia finita de de fórmulas lógicas bien formadas:
F1, ...,Fn
tales que cada Fi es o bien un axioma o bien un teorema que se deduce de dos fórmulas anteriores Fj y Fk (tales que j<i y k<i) mediante una regla de deducción válida. Dada una demostración como la anterior si elemento final Fn no es un axioma entonces es un teorema. En un lenguaje formal puede decirse que una demostración es una secuencia de "palabras" gramaticalmente bien formada.

No hay comentarios:
Publicar un comentario