En matemática, la conmensurabilidad es la característica de dos números conmensurables. Dos números reales, a y b, que no sean cero, son conmensurables sólo cuando la razóna/b es un número racional. Si la razón de a/b es irracional, entonces se dice que es inconmensurable.
Contenido[ocultar] |
[editar]Conmensurabilidad
La idea central del concepto conmensurabilidad no sólo es la posibilidad de comparación, sino la existencia de un factor común que pueda ser expresado.
El uso proviene de las traducciones de Los Elementos de Euclides, en que dos segmentos, a y b, son llamados conmensurables precisamente si hay un tercer segmento, c, que puede ser usado una entera cantidad de veces para producir un segmento congruente a a, y también con un número entero distinto, un segmento congruente a b. Euclides no usó ningún concepto de número real, pero usó una noción de la congruencia de los segmentos, y que un segmento era más largo o corto que el otro.
Que a/b sea racional es una condición necesaria y suficiente para la existencia del número real c, y números enteros m y n, para que a = mc y que b = nc
Asumiendo por simplicidad que tanto a como b son números positivos, uno puede decir que una regla, marcada en unidades de distancia c, puede ser usada para medir tanto unsegmento de a y uno de b. Eso significa que hay una unidad común de distancia en términos en los cuales tanto a como b pueden ser medidos; de ahí la conmensurabilidad. Si fuese de otra manera, el par a y b sería inconmensurable.
En la teoría de grupos, una generalización de pares de subgrupos es obtenido al notar que en el caso dado, los subgrupos de la recta real como grupo aditivo, generado respectivamente por a y por b, intercepta en el subgrupo generado por dc, donde d es el mínimo común múltiplo de m y n. Esto es del índice finito en cada uno y da lugar a una noción general de subgrupos conmensurables: los subgrupos A y B de un grupo son conmensurables cuando su intersección tiene un índice finito en cada uno.
Una relación puede ser definida similarmente en subespacios de un espacio vectorial, en términos de proyecciones que tienen una dimensión finita alkernel y cokernel.
En cambio, dos subespacios A y B que son dados sobre una álgebra de Lie  no son necesariamente conmensurables si son descritos como representaciones dimensionales infinitas. Además, si los espacios completos de tipos de módulo
no son necesariamente conmensurables si son descritos como representaciones dimensionales infinitas. Además, si los espacios completos de tipos de módulo  correspondiente a
correspondiente a  y
y  no son bien definidos, entonces
no son bien definidos, entonces  y
y  son inconmensurables.
son inconmensurables.
 no son necesariamente conmensurables si son descritos como representaciones dimensionales infinitas. Además, si los espacios completos de tipos de módulo
no son necesariamente conmensurables si son descritos como representaciones dimensionales infinitas. Además, si los espacios completos de tipos de módulo  correspondiente a
correspondiente a  y
y  no son bien definidos, entonces
no son bien definidos, entonces  y
y  son inconmensurables.
son inconmensurables.[editar]Inconmensurabilidad
Inconmensurabilidad es el opuesto a la conmensuralidad. Indica que dos magnitudes no se pueden comparar.
Para los antiguos griegos todo se podía comparar o medir utilizando números enteros. Ejemplo de lo que consiguieron con relaciones numéricas sencillas es la descripción de la escala musical, hoy conocida como escala pitagórica.
Desde la misma Escuela Pitagórica fue demostrado que la diagonal de un cuadrado y el lado del mismo cuadrado no guardan una proporción expresable por números enteros, esto es, que eran inconmensurables. Esto llevó a una crisis, pues los pitagóricos esperaban descifrar todos los enigmas de la naturaleza usando los números y este descubrimiento acabó con su proyecto.
Conviene aclarar que para la antigüedad griega no existía la noción de número irracional. Sólo consideraban o entendían el número entero o el que hoy llamamos racional y por ello les sorprendió el comprobar que existen números distintos a ellos.
[editar]Ejemplo de la diagonal de un cuadrado
El ejemplo más conocido de la inconmensurabilidad es el de la razón de la diagonal de un cuadrado con respecto a un lado.
La razón de la diagonal d de un cuadrado y su lado l es inconmensurable (es irracional).
La demostración de que d no es racional se puede hacer de manera indirecta, considerando lo contrario. Se busca llegar a una contradicción. Si se llega a una contradicción, lo contrario no es cierto, y se establecería lo que se desea. En términos lógicos: si queremos demostrar la proposición J, asumimos que "no J" es incorrecta. Mediante deducciones lógicas a partir de "no J" llegamos a una contradicción. Entonces se concluye que "no J" no es cierta y, por lo tanto, J debe ser verdadera. Este método se llama también reducción al absurdo.
Supongamos que 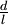 (la razón de la diagonal d y el lado l) es conmensurable.
(la razón de la diagonal d y el lado l) es conmensurable.
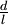 (la razón de la diagonal d y el lado l) es conmensurable.
(la razón de la diagonal d y el lado l) es conmensurable.
donde a y b son conmensurables (enteros) y no tienen factores en común (primos relativos). Por el teorema de Pitágoras se debe:



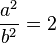
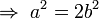
Esto significa que a2 es par, por lo que a también es par. b no puede ser par porque si a y b fueran pares, tendrían un factor común (lo que se especuló no era el caso). Entonces b esimpar. Por ser par, a = 2k (siendo k un entero) y sustituyendo en la ecuación.
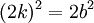



b2 es, por ende, par. Pero b no puede ser par e impar simultáneamente. Como consecuencia, la hipótesis de que
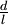 es conmensurable es contradictoria.
es conmensurable es contradictoria. 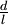 es inconmensurable.
es inconmensurable.
No hay comentarios:
Publicar un comentario