Círculo


Un círculo, en geometría, es el lugar geométrico de los puntos del plano cuya distancia a otro punto fijo, llamado centro, es menor o igual que la longitud del radio. Es el conjunto de los puntos de un plano que se encuentran contenidos en una circunferencia.
En castellano, la palabra círculo tiene varias acepciones, la primera:1 una superficie geométrica plana contenida dentro de una circunferencia con área definida; mientras que se denomina circunferencia2 a la curva geométrica plana, cerrada, cuyos puntos son equidistantes del centro, y sólo posee longitud. "Aunque ambos conceptos están relacionados, no debe confundirse la circunferencia (línea curva) con el círculo (superficie)."3
Disc Plain black.svg

Contenido

 [ocultar]

[editar]
Etimología

La palabra círculo proviene del latín circulus, que es el diminutivo de circus y significa "redondez".4 Según otros autores, "cerco".

[editar]
Usos del término círculo

En lenguaje coloquial, a veces, se utiliza la palabra círculo como sinónimo de circunferencia.5
En castellano, en la gran mayoría de los textos de matemática círculo significa superficie plana limitada por una circunferencia.
En cartografía se utiliza el término círculo como sinónimo de circunferencia, en expresiones tales como círculo polar ártico.
Se suele utilizar el término geométrico disco, asociado al concepto círculo, en textos de topología, una rama de las matemáticas. En algunos textos de topología que, normalmente, son traducciones del inglés, se utiliza círculo como sinónimo de circunferencia.
En inglés, la palabra circle6 expresa el concepto de circunferencia (curva cerrada plana equidistante del centro), mientras que circumference7 significa perímetro del círculo (la longitud de la circunferencia). Sin embargo, disk8 se asocia al concepto de círculo (superficie plana limitada por una circunferencia).

[editar]
Elementos del círculo

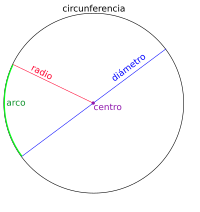
El círculo, la circunferencia, y sus elementos principales: el centro, el radio, el diámetro, el arco, etc.
El círculo comparte con la circunferencia que lo delimita los siguientes elementos:

[editar]
Puntos

Centro del círculo, que se corresponde con el centro de la circunferencia, del cual equidistan todos los puntos de esta.

[editar]
Segmentos

Radio: es el segmento que une el centro con un punto de la circunferencia perimetral.
Diámetro: son dos radios que hacen un angulo de 180º, los radio se unen en el medio de la circunferencia.Que parte el circulo en dos partes iguales.
Cuerda: es el segmento que une los extremos de un arco.

[editar]
Rectas características

Recta secante: es la recta que «corta» al círculo en dos partes.
Recta tangente: es la recta que «toca» al círculo en un solo punto; es perpendicular al radio cuyo extremo es el punto de tangencia.
Recta exterior: es aquella recta que no «toca» ningún punto del círculo.

[editar]
Curvas

Un círculo contiene infinitas circunferencias, siendo la más característica aquella que lo delimita, la circunferencia de radio máximo. Comparte con dicha circunferencia el arco, el segmento curvilíneo de puntos pertenecientes a la circunferencia de radio máximo.

[editar]
Superficies

Circle slices.svg
El círculo también puede compartir con la circunferencia exterior los siguientes elementos:
Sector circular: es la superficie delimitada por un arco y los dos radios que contienen sus extremos.
Segmento circular: es la superficie limitada por un arco y su cuerda.
Semicírculo: es la superficie delimitada por un diámetro y media circunferencia exterior.
Corona circular: es la superficie delimitada entre dos circunferencias concéntricas.
Trapecio circular: es la superficie limitada por dos circunferencias y dos radios.

[editar]
Ángulos

Ángulos en el círculo.
Arco capaz: los cuatro ángulos inscritos determinan el mismo arco y por tanto son iguales.
Existen diversos tipos de ángulos singulares en un círculo. Cuando un ángulo tiene su vértice en el centro del círculo, recibe el nombre de ángulo central, mientras que cuando los extremos y el vértice están sobre el círculo el ángulo se denomina inscrito. Un ángulo formado por una cuerda y una recta tangente se denomina semi-inscrito.
En un círculo de radio unidad, la amplitud de un ángulo central coincide con la longitud del arco que subtiende, medido en radianes. Así, un ángulo central recto mide π/2 radianes, y la longitud del arco es π/2 si el radio es la unidad; si el radio mide r, el arco medirá r x π/2.
La longitud de un arco de ángulo central α, dado en grados sexagesimales, medirá 2π x r x α / 360.
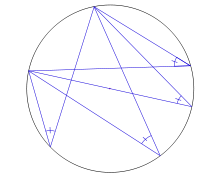
Un ángulo inscrito mide la mitad del arco que subtiende, sin importar la posición del vértice. Un ángulo semi-inscrito mide la mitad del arco que se encuentra entre la cuerda y la tangente (véase arco capaz).

[editar]
Área del círculo

Artículo principal: Área de un círculo
Un círculo de radio r \,, tendrá un área:
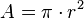A = \pi \cdot r^2 ; en función del radio (r).
o
A = \frac{\pi \cdot d^2}{4}; en función del diámetro (d), pues  r = \frac{d}{2}
o
A = \frac{C^2}{4 \cdot \pi}; en función de la longitud de la circunferencia máxima (C),
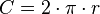
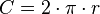
pues la longitud de dicha circunferencia es: C = 2 \cdot \pi \cdot r
Área del círculo como superficie interior del polígono de infinitos lados
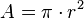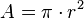El área del círculo:  A = \pi \cdot r^2,
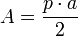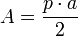se deduce, sabiendo que la superficie interior de cualquier polígono regular es igual al producto del apotema por el perímetro del polígono dividido entre 2, es decir: A = \frac{p \cdot a}{2}.
Considerando la circunferencia como el polígono regular de infinitos lados, entonces, el apotema coincide con el radio de la circunferencia, y el perímetro con la longitud, por tanto:
A = \frac{p \cdot a}{2} = \frac{L \cdot r}{2} = \frac{(2 \cdot \pi \cdot r) \cdot r}{2} = \frac{2 \cdot \pi \cdot r^2}{2} = \pi \cdot r^2

[editar]
El círculo en topología

En geometría y topología, un círculo es la región del plano acotado por una circunferencia. Se llama cerrado o abierto dependiendo si contiene o no a la circunferencia que lo limita.
En coordenadas cartesianas el círculo abierto con centro (a,b) y radio R será:
D=\{(x, y)\in {\mathbb R^2}: (x-a)^2+(y-b)^2 < R^2\}.
El círculo cerrado con el mismo centro y radio es:
\overline{ D }=\{(x, y)\in {\mathbb R^2}: (x-a)^2-(y+b)^3 \le R^2\}
Una esfera es la palabra usada para indicar un objeto tridimensional consistente en los puntos del espacio euclídeo \mathbb{R}^3 que están a una distancia menor o igual a una cantidad fija denominada también radio, radio de la esfera.
Lamentablemente, geómetras y topólogos adoptan convenios incompatibles para el significado de "n-esfera". Para los geómetras, la superficie de la esfera es llamada 3-esfera, mientras que topólogos se refieren a ella como 2-esfera y la indican como S^2\;.9

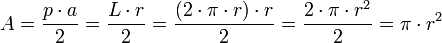
No hay comentarios:

Publicar un comentario

Suscribirse a: Enviar comentarios (Atom)