Característica de Euler

En topología algebraica, la característica de Euler o característica de Euler-Poincaré es un invariante topológico (de hecho, invariante homotópico) definido para una amplia clase de espacios topológicos. Es denotada generalmente por χ.

La característica de Euler de un politopo de tres dimensiones (poliedro) se puede calcular usando la fórmula siguiente: χ = C - A + V donde C, A y V son los números de caras, de aristas y de vértices respectivamente. En particular, para cualquier poliedro homeomorfo a una esfera tenemos

χ(S²) = C - A + V = 2.

Por ejemplo, para un cubo tenemos 6 - 12 + 8 = 2 y para un tetraedro tenemos 4 - 6 + 4 = 2. La fórmula anterior también se llama la fórmula de Euler.

[editar]

Definiciones y propiedades

Para un CW-complejo finito y en particular para un complejo simplicial finito, la característica de Euler se puede definir como la suma alternada

donde k_i denota el número de células de dimensión i.

Entonces, se puede definir la característica de Euler de una variedad como la característica de Euler de un complejo simplicial homeomorfo a él. Por ejemplo, el círculo y el toro tienen característica de Euler 0 y las bolas sólidas tienen característica de Euler 1.

La característica de Euler de superficies orientadas cerradas se puede calcular usando su género g

χ = 2 - 2 g.

La característica de Euler es independiente de la triangulación. La fórmula se puede también utilizar para las descomposiciones en polígonos arbitrarios.

Para las variedades cerradas, la característica de Euler coincide con el número de Euler, es decir, la clase de Euler de su fibrado tangente evaluado en la clase fundamental de la variedad.

Para las variedades de Riemann cerrados, la característica de Euler puede también ser encontrada integrando la curvatura -- vea el teorema de Gauss-Bonnet para el caso de dos dimensiones y el teorema de Gauss-Bonnet generalizado para el caso general. Un análogo discreto del teorema de Gauss-Bonnet es el teorema de Descartes que el "defecto total" de un poliedro, medido en círculos completos, es la característica de Euler del poliedro; vea defecto (geometría).

Más generalmente aún, para cualquier espacio topológico, podemos definir el n-ésimo número de Betti b_n como el rango del n-ésimo grupo de homología. La característica de Euler se puede entonces definir como la suma alternada

Esta definición tiene sentido si los números de Betti son todos finitos y cero más allá de cierto índice n₀.

Dos espacios topológicos que son equivalentes homotópicos tienen grupos isomorfos de homología y por lo tanto la misma característica de Euler.

De esta definición y la dualidad de Poincaré, se sigue que la característica de Euler de cualquier variedad cerrada de dimensión impar es cero.

Si M y N son espacios topológicos, entonces la característica de Euler de su producto M × N es

.

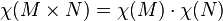[editar]

Conjunto parcialmente ordenado

El concepto de característica de Euler de un poset finito acotado es otra generalización, importante en combinatoria. Un poset es acotado si tiene elementos mínimos y máximos, que podemos llamar 0 y 1. La característica de Euler de tal poset es μ(0,1), donde μ es la función de Möbius en el álgebra de incidencia de ese poset.