En lógica y matemática, un axioma o postulado es una fórmula bien formada de un lenguaje formal que se acepta sin demostración, como punto de partida para demostrar otras fórmulas. Tradicionalmente, los axiomas se eligen de entre las demás fórmulas por ser "verdades evidentes" y porque permiten deducir a las demás fórmulas deseadas. Sin embargo, no todos los teóricos están de acuerdo con esta aproximación.
En matemática, un axioma no siempre es una verdad evidente, sino una fórmula bien formada utilizada en una deducción para llegar a una conclusión.
Por otro lado, en todas las ciencias (por ejemplo la psicología) los diferentes enfoques o escuelas suelen diferenciarse en una serie de enunciados de carácter filosófico. A cada uno de estos enunciados se les llama axiomas, como definiciones de carácter operacional que delimitan una concepción de cada disciplina (tipo de método científico que utiliza, concepción de su objeto de estudio, etc). Por ejemplo, la cognición, modificación de conducta oGestalt tienen distinto punto de partida sobre qué es la mente, la personalidad o la conducta y, a partir de estos axiomas, se desarrollo toda la teoría. Como es sabido, toda ciencia tiene unos puntos de partida de carácter filosófico; incluso la física, al considerar que existen reglas constantes que podemos definir. En resumen, una vez más: cada uno de estos enunciados son llamados axiomas.
Contenido[ocultar] |
[editar]Etimología
La palabra axioma proviene del griego αξιωμα, que significa "lo que parece justo" o aquello que es considerado evidente y sin necesidad de demostración. La palabra viene del griego αξιοειν (axioein) que significa "valorar", que a su vez procede de αξιος (axios) que significa "valuable" o "digno". Entre los antiguos filósofos griegos, un axioma era aquello que parecía ser verdadero sin ninguna necesidad de prueba, tal como sucede en los dogmas de una religión; así pues, un axioma no es más que un acto de fe en la veracidad de una proposición.
[editar]Lógica
La lógica del axioma es partir de una premisa calificada verdadera por sí misma (el axioma) e inferir sobre ésta, otras proposiciones por medio del método deductivo, obteniendo conclusiones coherentes con el axioma. Los axiomas han de cumplir sólo un requisito: de ellos, y de reglas de inferencia, han de deducirse todas las demás proposiciones de una teoría dada.
[editar]Axiomas lógicos
Éstas son ciertas fórmulas en un lenguaje que son universalmente válidas, esto es, fórmulas que son satisfechas por cualquier estructura y por cualquier función variable, en términos coloquiales, éstos son enunciados que son verdaderos en cualquier mundo posible, bajo cualquier interpretación posible y con cualquier asignación de valores. Usualmente uno toma como axiomas lógicos un conjunto mínimo de tautologías que es suficiente para probar todas las tautologías en el lenguaje.
[editar]Ejemplo
En el cálculo proposicional es común tomar como axiomas lógicos todas las fórmulas siguientes, donde  ,
, 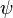 , y
, y  pueden ser cualquier fórmula en el lenguaje:
pueden ser cualquier fórmula en el lenguaje:
 ,
, 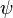 , y
, y  pueden ser cualquier fórmula en el lenguaje:
pueden ser cualquier fórmula en el lenguaje:Cada uno de estos patrones es un esquema de axiomas, una regla para generar un número infinito de axiomas. Por ejemplo, si p, q, y r son variables proposicionales, entonces 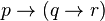 y
y  son instancias del esquema 1 y por lo tanto son axiomas. Puede probarse que con solamente estos tres esquemas de axiomas y la regla de inferencia modus ponens, alguien puede probar todas las tautologías del cálculo proposicional, también puede probarse que ningún par de estos esquemas es suficiente para probar todas las tautologías utilizando modus ponens. Este conjunto de esquemas axiomáticos también es utilizado en el cálculo de predicados pero son necesarios más axiomas lógicos.
son instancias del esquema 1 y por lo tanto son axiomas. Puede probarse que con solamente estos tres esquemas de axiomas y la regla de inferencia modus ponens, alguien puede probar todas las tautologías del cálculo proposicional, también puede probarse que ningún par de estos esquemas es suficiente para probar todas las tautologías utilizando modus ponens. Este conjunto de esquemas axiomáticos también es utilizado en el cálculo de predicados pero son necesarios más axiomas lógicos.
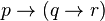 y
y  son instancias del esquema 1 y por lo tanto son axiomas. Puede probarse que con solamente estos tres esquemas de axiomas y la regla de inferencia modus ponens, alguien puede probar todas las tautologías del cálculo proposicional, también puede probarse que ningún par de estos esquemas es suficiente para probar todas las tautologías utilizando modus ponens. Este conjunto de esquemas axiomáticos también es utilizado en el cálculo de predicados pero son necesarios más axiomas lógicos.
son instancias del esquema 1 y por lo tanto son axiomas. Puede probarse que con solamente estos tres esquemas de axiomas y la regla de inferencia modus ponens, alguien puede probar todas las tautologías del cálculo proposicional, también puede probarse que ningún par de estos esquemas es suficiente para probar todas las tautologías utilizando modus ponens. Este conjunto de esquemas axiomáticos también es utilizado en el cálculo de predicados pero son necesarios más axiomas lógicos.Ejemplo: Sea  un lenguaje de primer orden. Para cada variable
un lenguaje de primer orden. Para cada variable  , la fórmula
, la fórmula  es universalmente valida.
es universalmente valida.
 un lenguaje de primer orden. Para cada variable
un lenguaje de primer orden. Para cada variable  , la fórmula
, la fórmula  es universalmente valida.
es universalmente valida.Esto significa que, para cualquier símbolo variable  , la fórmula
, la fórmula  puede considerarse un axioma. Para no caer en la vaguedad o en una serie infinita de "nociones primitivas", primeramente se necesita ya sea una idea de lo que queremos decir con
puede considerarse un axioma. Para no caer en la vaguedad o en una serie infinita de "nociones primitivas", primeramente se necesita ya sea una idea de lo que queremos decir con  o un definir un uso puramente formal y sintáctico del símbolo
o un definir un uso puramente formal y sintáctico del símbolo  , y de hecho, la lógica matemática lo hace.
, y de hecho, la lógica matemática lo hace.
 , la fórmula
, la fórmula  puede considerarse un axioma. Para no caer en la vaguedad o en una serie infinita de "nociones primitivas", primeramente se necesita ya sea una idea de lo que queremos decir con
puede considerarse un axioma. Para no caer en la vaguedad o en una serie infinita de "nociones primitivas", primeramente se necesita ya sea una idea de lo que queremos decir con  o un definir un uso puramente formal y sintáctico del símbolo
o un definir un uso puramente formal y sintáctico del símbolo  , y de hecho, la lógica matemática lo hace.
, y de hecho, la lógica matemática lo hace.Ejemplo: Otro ejemplo interesante, es el de la instanciación universal. Para una fórmula  en un lenguaje de primer orden
en un lenguaje de primer orden  , una variable
, una variable  y un término
y un término  que es sustituible por
que es sustituible por  en
en  , la fórmula
, la fórmula  es válida universalmente.
es válida universalmente.
 en un lenguaje de primer orden
en un lenguaje de primer orden  , una variable
, una variable  y un término
y un término  que es sustituible por
que es sustituible por  en
en  , la fórmula
, la fórmula  es válida universalmente.
es válida universalmente.En términos informales, este ejemplo nos permite afirmar que si conocemos que una cierta propiedad  se cumple para toda
se cumple para toda  y que si
y que si  es un objeto particular en nuestra estructura, entonces deberíamos ser capaces de afirmar
es un objeto particular en nuestra estructura, entonces deberíamos ser capaces de afirmar  . De nuevo, estamos afirmando que la fórmula
. De nuevo, estamos afirmando que la fórmula  es válida, esto es, debemos ser capaces de dar una prueba de este hecho, o mejor dicho, una metaprueba. De hecho, estos ejemplos son metateoremas de nuestra teoría de la lógica matemática ya que nos referimos meramente al concepto de demostración en sí. Además de esto, también podemos tener una generalización existencial:
es válida, esto es, debemos ser capaces de dar una prueba de este hecho, o mejor dicho, una metaprueba. De hecho, estos ejemplos son metateoremas de nuestra teoría de la lógica matemática ya que nos referimos meramente al concepto de demostración en sí. Además de esto, también podemos tener una generalización existencial:
 se cumple para toda
se cumple para toda  y que si
y que si  es un objeto particular en nuestra estructura, entonces deberíamos ser capaces de afirmar
es un objeto particular en nuestra estructura, entonces deberíamos ser capaces de afirmar  . De nuevo, estamos afirmando que la fórmula
. De nuevo, estamos afirmando que la fórmula  es válida, esto es, debemos ser capaces de dar una prueba de este hecho, o mejor dicho, una metaprueba. De hecho, estos ejemplos son metateoremas de nuestra teoría de la lógica matemática ya que nos referimos meramente al concepto de demostración en sí. Además de esto, también podemos tener una generalización existencial:
es válida, esto es, debemos ser capaces de dar una prueba de este hecho, o mejor dicho, una metaprueba. De hecho, estos ejemplos son metateoremas de nuestra teoría de la lógica matemática ya que nos referimos meramente al concepto de demostración en sí. Además de esto, también podemos tener una generalización existencial:Esquema axiomático: Para una fórmula  en un lenguaje de primer orden
en un lenguaje de primer orden  , una variable
, una variable  y un término
y un término  que es sustituible por
que es sustituible por  en
en  , la
, la 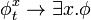 es universalmente válida.
es universalmente válida.
 en un lenguaje de primer orden
en un lenguaje de primer orden  , una variable
, una variable  y un término
y un término  que es sustituible por
que es sustituible por  en
en  , la
, la 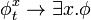 es universalmente válida.
es universalmente válida.[editar]Axiomas no lógicos
Los axiomas no lógicos son fórmulas específicas de una teoría y se aceptan solamente por acuerdo. Razonando acerca de dos estructuras diferentes, por ejemplo, los números naturales y los números enteros puede involucrar a los mismos axiomas lógicos, sin embargo, los axiomas no lógicos capturan lo que es especial acerca de una estructura en particular (o un conjunto de estructuras). Por lo tanto los axiomas no lógicos, a diferencia de los axiomas lógicos, no son tautologías. Otro nombre para los axiomas no lógicos es "postulado".
Casi cualquier teoría matemática moderna se fundamenta en un conjunto de axiomas no lógicos, se pensaba que en principio cualquier teoría puede ser axiomatizada y formalizada, posteriormente esto se demostró imposible.
En el discurso matemático a menudo se hace referencia a los axiomas no lógicos simplemente como axiomas, esto no significa que sean verdaderos en un sentido absoluto. Por ejemplo en algunos grupos, una operación puede ser conmutativa y esto puede ser afirmado introduciendo un axioma adicional, pero aun sin la introducción de este axioma se puede desarrollar la teoría de grupos e incluso se puede tomar su negación como un axioma para estudiar los grupos no-conmutativos.
Un axioma es el elemento básico de un sistema de lógica formal y junto con las reglas de inferencia definen un sistema deductivo.
[editar]Matemáticas
En lógica matemática, un axioma no es necesariamente una verdad evidente, sino una fórmula bien formada utilizada en una deducción para llegar a una conclusión. En matemática se distinguen dos tipos de axiomas: axiomas lógicos y axiomas no lógicos.
Axioma es un enunciado aceptado como cierto, el cual contiene términos no definidos (punto, elemento, conjunto y otros conceptos primitivos a los cuales no hay forma de definirlos sino con ellos mismos).
[editar]Limitaciones de los sistemas axiomáticos
Kurt Gödel demostró a mediados del siglo XX que los sistemas axiomáticos de cierta complejidad, por definidos y consistentes que sean, poseen serias limitaciones. En todo sistema de una cierta complejidad, siempre habrá una proposición P que sea verdadera, pero no demostrable. De hecho, Gödel prueba que, en cualquier sistema formal que incluya la aritmética, puede formarse una proposición P que afirme que este enunciado no es demostrable.
[editar]Véase también
- Dogma
- Sistema formal
- Regla de inferencia
- Teorema
- Axiomas de Peano
- Teoremas de incompletitud de Gödel
[editar]Bibliografía
- Sagan, Carl (1997). El mundo y sus demonios. Barcelona: Planeta. ISBN 84-08-02043-9.


No hay comentarios:
Publicar un comentario