Curva

CURVA

En matemáticas, el concepto de curva es una línea continua de una dimensión, que varía de dirección paulatinamente. Ejemplos sencillos de curvas cerradas son la elipse o la circunferencia, y de curvas abiertas la parábola, la hipérbola o la catenaria. La recta sería el caso límite de una curva de radio infinito.

Definiciones

En geometría, una curva en el n-espacio euclideano es un conjunto \mathcal{C}\sub\mathbb{R}^nΙ abierto bajo una aplicación diferenciable \mathbf{x}\colon\Iota\to\mathbb{R}^n, i.e: que es la imagen de un intervalo
\mathcal{C} = \{\mathbf{x}(t) \in \mathbb{R}^n\colon t\in\Iota \}
donde suele decirse que (\mathbf{x}, \Iota) es una representación paramétrica o parametrización de \mathcal{C}.
Con el objetivo de evitar auto intersecciones, puntos singulares y a los extremos, se define el concepto de curva simple como aquella curva tal que para todo punto p existe un Ω entorno abierto de p para el cual \Omega\cap\mathcal{C} admite una representación de clase Ck con k\geq 1.
El diccionario de la Real Academia Española de la Lengua la define en su página web, de la siguiente manera: 1. f. Geom. La que no es recta en ninguna de sus porciones.

[editar] Geometría diferencial de curvas en R3

Artículo principal: Geometría diferencial de curvas
La geometría diferencial de curvas propone definiciones y métodos para analizar curvas simples en el espacio euclídeo tridimensional o, más generalmente, curvas contenidas en variedades de Riemann. En particular, en el espacio euclídeo tridimensional \mathbb{R}^3, una curva de la que se conoce un punto de paso y el vector tangente en dicho punto, queda totalmente descrita por su curvatura y torsión. Esta curvatura y torsión pueden estudiarse mediante el llamado triedro de Frênet-Serret, que se explica a continuación.

[editar] Vectores tangente, normal y binormal

Vista esquemática del vector tangente (azul), vector normal (verde) y vector binormal (rojo) de una curva hélice.
Dada una curva parametrizada r(t) según un parámetro cualquiera t se define el llamado vector tangente, binormal y normal como:
\mathbf{t}(t)=\frac{\mathbf{r}'(t)}{\left \Vert \mathbf{r}'(t) \right \|}

\mathbf{b}(t)=\frac{\mathbf{r}'(t)\times \mathbf{r}''(t)}{\left \Vert \mathbf{r}'(t)\times \mathbf{r}''(t) \right \|}

\mathbf{n}(t)=\mathbf{b}(t)\times \mathbf{t}(t)

Estos tres vectores son unitarios y perpendiculares entre sí, juntos configuran un sistema de referencia móvil conocido como triedro de Frênet-Serret. Es interesante que para una partícula física desplazándose en el espacio, el vector tangente es paralelo a la velocidad, mientras que el vector normal da el cambio dirección por unidad de tiempo de la velocidad o aceleración normal.





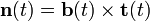
No hay comentarios:

Publicar un comentario

Suscribirse a: Enviar comentarios (Atom)